Par Florent Gbongué*
La courbe des taux sans risque est un véritable outil d’appréciation de la valeur de l’argent à travers le temps. Elle sert aussi de référence aux émetteurs intervenant sur les marchés financiers et constitue un excellent outil d’optimisation de la politique monétaire des banques centrales. En Afrique subsaharienne francophone, cette courbe est pratiquement absente.
Dans cet article, nous nous intéresserons à la forme de la courbe des taux sans risque adaptée au contexte de la zone CIPRES*. En pratique, nous décrirons en premier lieu le marché financier de la CIPRES. En second lieu, nous nous interrogerons sur la forme de la courbe des taux sans risque, ainsi que son comportement asymptotique. Enfin, notre application numérique portera sur les obligations d’états des pays de la zone CIPRES. Mots-clés : Courbe des taux, marchés financiers, CIPRES, modèles d’interpolation, d’extrapolation, BRVM.
La courbe des taux sans risque ou de rendement (en anglais yield curve) d’une obligation financière est la fonction qui, à une date donnée et pour chaque maturité (son échéance), indique le niveau de taux d’intérêt associé. On la représente sur un repère dont l’axe des abscisses correspond à la maturité de l’obligation et l’ordonnée au taux d’intérêt. Elle répond à deux demandes sur les marchés financiers puisque, d’un côté, elle agrège l’ensemble des taux d’intérêt que va devoir acquitter un émetteur et, de l’autre, elle informe les investisseurs des rendements d’un titre selon sa maturité. La structure et l’évolution de la courbe sont donc des informations cruciales pour l’efficience des marchés obligataires (cf. ALLOUCHE [2013]). Si elle joue un rôle important sur les marchés financiers ; en revanche elle est aussi utile pour les entreprises, les banques et les compagnies d’assurance. En effet, la courbe des taux sans risque permet de déduire les facteurs d’actualisation, reflétant ainsi la valeur future d’une série de flux financiers. En assurance, elle permet d’estimer finement les engagements des compagnies d’assurance et d’optimiser leur politique d’investissement (ALM). Dans le secteur bancaire, cette courbe est fondamentale dans l’élaboration d’un système interne de tarification des « business lines ».
En effet, la courbe des taux sans risque permet de déduire les facteurs d’actualisation, reflétant ainsi la valeur future d’une série de flux financiers. En assurance, elle permet d’estimer finement les engagements des compagnies d’assurance et d’optimiser leur politique d’investissement (ALM).
Vue synoptique des marchés financiers dans la zone CIPRES
Organisme de contrôle et d’appui technique aux Caisses Africaines de Sécurité Sociale, la Conférence Interafricaine de la Prévoyance Sociale (CIPRES) regroupe les quinze (15) pays suivants : Le Benin, le Burkina Faso, le Cameroun, la Centrafrique, le Comores, le Congo (Brazzaville), la RD Congo, la Côte d’Ivoire, le Gabon, la Guinée équatoriale, le Mali, le Niger, le Sénégal, le Tchad et le Togo. L’analyse du contexte économique de la CIPRES montre que certains pays possèdent leur propre espace économique en occurrence l’Union économique et monétaire ouest africaine (UEMOA) et la Communauté économique et monétaire de l’Afrique centrale (CEMAC); tandis que le Comores et la RD Congo ne sont affiliés à aucun espace économique. Ainsi, nous pouvons observer dans la zone CIPRES, les marchés financiers de l’UEMOA, de la CEMAC, du Comores et de la RD Congo.
L’UEMOA
Nous retrouvons principalement, dans l’UEMOA, le Marché Financier Régional (MFR) qui coexiste avec les marchés interbancaire, monétaire et des changes. Le MFR est un marché unique regroupant l’ensemble des pays membres de l’Union Monétaire Ouest Africaine (UMOA) à savoir le Bénin, le Burkina Faso, la Côte d’Ivoire, la Guinée Bissau, le Mali, le Niger, le Sénégal et le Togo. Le MFR a été conçu pour compléter et renforcer les marchés interbancaires et monétaires et offrir aux opérateurs économiques de la sous région de nouvelles opportunités de placement et de financement alternatifs. Le marché financier de l’UEMOA fait intervenir un ensemble d’acteur et est organisé autour de deux pôles essentiels :
-Un pôle privé, composé de la Bourse Régionale des Valeurs Mobilières et du Dépositaire Central/Banque de Règlement ainsi que des intervenants commerciaux, à savoir les Sociétés de Gestion et d’Intermédiation, les Sociétés de gestion de patrimoine, les Apporteurs d’Affaires, les Sociétés de Conseils en Valeurs Mobilières et les démarcheurs ;
-Un pôle public, symbolisé par le Régulateur communautaire du marché en l’occurrence le Conseil Régional de l’Epargne Publique et des Marchés Financiers (CREPMF). Celui-ci représente l’intérêt général et garantit la sécurité et l’intégrité du marché. L’univers des investissements est composé principalement des actions et des obligations.
Sur la BRVM, nous notons que la capitalisation boursière du marché des actions est passée de 1 108 milliards de FCFA en 1998 à 3553 milliards de FCFA au 31 octobre 2012, soit une progression de plus de 220 % depuis le démarrage des activités de la Bourse. Par contre celle des obligations est passée de 83 milliards de FCFA en 1999 à 1017,44 milliards de FCFA au 18 juin 2013, soit une progression de plus de 1125,83 % depuis le démarrage des activités de la Bourse.
La CEMAC
La structure du marché financier de la CEMAC est semblable à celle de l’UEMOA. Toutefois, le marché financier régional de la CEMAC n’est pas intégré. Il comprend deux places financières que sont la bourse des valeurs mobilières de l’Afrique centrale (BVMAC) et la bourse de Douala (DSX), ainsi que deux autorités de tutelle en occurrence la Commission de Surveillance du Marché Financier de l’Afrique centrale (COSUMAF) et la Commission des Marchés Financiers (CMF).
Le Comores
Le secteur financier des Comores est relativement petit et peu développé. Il est constitué d’une banque centrale (BCC), de deux banques commerciales (dont la plus grande, à savoir la Banque pour l’industrie et le commerce des Comores, est la propriété de la BNP Paribas), d’une banque de développement, et de deux réseaux d’IMF (les Mecks et les Sanduks) (cf. BAD [2010]).
La République démocratique du Congo
Le marché financier de la RDC est régulé par la Banque centrale du Congo (BCC). Par comparaison au marché de l’UEMOA, nous pouvons le restreindre au marché monétaire sur lequel la BCC émet des obligations et des bons du trésor sur des maturités courtes (inférieur à 29 jours).
Forme de la courbe des taux sans risque dans la zone CIPRES. Nous nous intéresserons dans cette section à la forme de la courbe des taux sans risque dans la zone CIPRES. Dans les pays développés, Il existe plusieurs institutions qui fournissent des courbes de taux sans risque, servant de référence aux professionnels de la finance.
Par exemple, les courbes de référence rencontrées en Europe sont construites selon les méthodes de l’EIOPA, de l’institut des actuaires (IA), du Comité de Normalisation Obligataire (CNO) et de la FINMA dans le cadre du « Swiss Solvency Test (SST) ». En pratique, les modèles mathématiques utilisés pour construire ces courbes sont les modèles de Nelson Siegel (1987), Vacicek-fong (1982) et de Smith Wilson (2001).
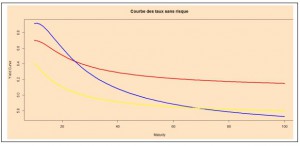
Dans le contexte de la zone CIPRES, nous avons utilisé le modèle de Nelson Siegel (1987) pour construire la courbe des taux sans risque. Nous allons étudier par la suite, le comportement de cette courbe sur deux parties à savoir la partie observable (0 à 10 ans) et la partie non observable (> 10 ans). En pratique, nous analyserons le comportement de trois courbes des taux sans risque aux dates de cotation 31.12.2014, 31.01.2015 et 27.02.2015, représentées respectivement par les couleurs rouge, bleu et jaune.
Forme de la courbe des taux sans risque dans la zone CIPRES
Nous nous intéresserons dans cette section à la forme de la courbe des taux sans risque dans la zone CIPRES. Dans les pays développés, Il existe plusieurs institutions qui fournissent des courbes de taux sans risque, servant de référence aux professionnels de la finance. Par exemple, les courbes de référence rencontrées en Europe sont construites selon les méthodes de l’EIOPA, de l’institut des actuaires (IA), du Comité de Normalisation Obligataire (CNO) et de la FINMA dans le cadre du « Swiss Solvency Test (SST) ». En pratique, les modèles mathématiques utilisés pour construire ces courbes sont les modèles de Nelson Siegel (1987), Vacicek-fong (1982) et de Smith Wilson (2001). Dans le contexte de la zone CIPRES, nous avons utilisé le modèle de Nelson Siegel (1987) pour construire la courbe des taux sans risque. Nous allons étudier par la suite, le comportement de cette courbe sur deux parties à savoir la partie observable (0 à 10 ans) et la partie non observable (> 10 ans). En pratique, nous analyserons le comportement de trois courbes des taux sans risque aux dates de cotation 31.12.2014, 31.01.2015 et 27.02.2015, représentées respectivement par les couleurs rouge, bleu et jaune.
Evolution de la courbe de taux sans risque sur la partie non observable [10 – 100 ans]
Le débat se situe sur le comportement asymptotique de la courbe des taux sans risque au-delà de la dernière maturité liquide ou « Last Liquid point (LLP) ». Dans les pays européens, l’EIOPA par exemple, suggère d’utiliser la méthode de Smith Wilson pour extrapoler la courbe au delà du LLP. Un autre exemple est celui proposé par Barrie & Hilbert (2010) qui utilise une technique de regression spline sur la partie observable et la méthode de Nelson Siegel sur la partie non observable (cf. ANTONIO et ROSEBURGH [2010]).
Par contre, dans la zone CIPRES, la question reste poser. Une approche simple sera d’utiliser comme en Europe la méthode de Smith Wilson pour déterminer le comportement asymptotique de la courbe. In fine, le choix du modèle mathématique et du mode de convergence de la courbe reflèteront la forme que nous voulons lui donner sur la partie non observable. Si nous utilisons le modèle de Nelson Siegel sur la partie non observable, nous remarquons que les taux sans risque baissent progressivement avant de converger vers le « Ultimate Forward Rate », voir la figure ci-dessous :
Evolution de la courbe de taux sans risque sur les deux parties [0 – 100 ans]
La forme de la courbe des taux sans risque dépend du choix du modèle mathématique et de la stratégie de convergence de la courbe sur le long terme. Nous avons utilisé dans cet article le modèle de Nelson Siegel (1987) pour construire une courbe des taux sans risque pertinente pour la zone CIPRES. Ainsi, nous avons vu que la courbe obtenue était croissante sur la partie observable (0 à 10 ans) pour les jours de cotation 31.12.2014, 31.12.2015 et 27.02.2015. Cette forme de la courbe est en accord avec la théorie des anticipations de la structure par terme des taux d’intérêt (cf. Hicks [1939]). Par contre, elle commence à décroitre sur la partie non observable à partir de la maturité 11 ans, ce qui coïncide avec les pratiques actuelles du marché, notamment dans le secteur bancaire. Le débat reste donc ouvert sur le modèle à utiliser pour extrapoler la courbe au delà de la dernière maturité liquide et du point de convergence des taux sur le long terme.
Conclusion
La forme de la courbe des taux sans risque dépend du choix du modèle mathématique et de la stratégie de convergence de la courbe sur le long terme. Nous avons utilisé dans cet article le modèle de Nelson Siegel (1987) pour construire une courbe des taux sans risque pertinente pour la zone CIPRES. Ainsi, nous avons vu que la courbe obtenue était croissante sur la partie observable (0 à 10 ans) pour les jours de cotation 31.12.2014, 31.12.2015 et 27.02.2015. Cette forme de la courbe est en accord avec la théorie des anticipations de la structure par terme des taux d’intérêt (cf. Hicks [1939]). Par contre, elle commence à décroitre sur la partie non observable à partir de la maturité 11 ans, ce qui coïncide avec les pratiques actuelles du marché, notamment dans le secteur bancaire. Le débat reste donc ouvert sur le modèle à utiliser pour extrapoler la courbe au delà de la dernière maturité liquide et du point de convergence des taux sur le long terme.
–Florent Gbongué est doctorant au laboratoire de Science actuarielle et financière et Expert en Risk-Management à la SIB – groupe ATTIJARIWAFA BANK. Contact : florent.gbongue@gmail.com
-Institut de Science Financière et d’Assurances (ISFA) – 50 avenue Tony Garnier – 69366 Lyon Cedex 07 – France.
-Société Ivoirienne de Banque (SIB) – 34 bd République, immeuble Alpha 2000.
-CIPRES: conférence interafricaine de la prévoyance sociale, regroupe 15 pays de l’Afrique de l’Ouest et du Centre.
Bibliographie
Allouche J. (2013) : La courbe des taux. BSI Economics. Antonio D.,
Roseburgh D. (2010): Fitting the Yield Curve Cubic spline interpolation and smooth extrapolation.
Barrie + Hilbert Calibration.
Banque Africaine de Développement (2010): Guide des marchés obligataires africains et des produits dérivés.
CEIOPS (2010). Qis 5 risk-free interest rates extrapolation method. Technical report, CEIOPS
FINANSTILSYNET (2010): A Technical Note on the Smith-Wilson Method. Gilli, M., Grosse, S., and Schumann, E. (2010). Calibrating the Nelson-Siegel Svensson model. Available at SSRN 1676747. Nelson C. R., Siegel A. F.
(1987): Parsimonious modeling of yield curves”, Journal of business, Vol 60, 473-489 Smith, A., & Wilson, T. (2001). Fitting yield curves with long term constraints. (Research Notes, Bacon and Woodrow. Referred to in Thomas, M. and Mar ́e, E. (2007)) Vasicek, O., & Fong, H. G. (1982).
Term structure modeling using exponential splines. The Journal of Finance, 37 (2), 339–348.